Computer History

“Who Invent the Computer?”
That’s very tough question. The invention of a computer is a process, there’s many people and invention to contribute in the process that make computer development like today. So, it’s more like history than to say, Someone found a computer at first time.

The computer history was start at very beginning. It dated back when people start to count. And the process still going. We don’t know what’s computer will be in the next future. But here we are, can’t live without this device in our daily.

Here’s  computer timeline history, to remind us that work is still in progress:

30,000 BC

Starting a very long time ago, people in paleolithic era (which live in caves or forests) in central Europe, recording number by making a tally in animal bones, ivory and stones. This is a starting point to “compute”.

3400 BC

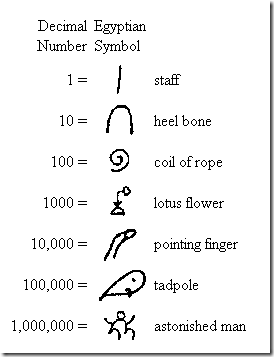
The Egypt develop a symbol for the number 10, this simplifying the representation of large number

2600 BC

The Chinese abacus and zhusuan (reckoning by the abacus) were created by a famous mathematician Cheng Dawei of the Ming Dynasty (1368-1644), known worldwide as "the great master of zhusuan". In Japan, he is worshipped as "the God of Arithmetics," and August 8 was established as the "abacus festival" in commemoration of him.

300 BC

Euclid, A Greek Mathematician, release his books. Euclids Elements.

Euclid's Elements  is a mathematical and geometric treatise consisting of 13 books . It is a collection of definitions, postulates (axioms), propositions (theorems and constructions), and mathematical proofs of the propositions. The thirteen books cover Euclidean geometry and the ancient Greek version of elementary number theory. With the exception of Autolycus' On the Moving Sphere, the Elements is one of the oldest extant Greek mathematical treatises and it is the oldest extant axiomatic deductive treatment of mathematics. It has proven instrumental in the development of logic and modern science.

[Picture above ] The frontispiece of Sir Henry Billingsley's first English version of Euclid's Elements, 1570

260 BC

The Mayan develop a  base-20 system of mathematical that includes zero. It’s used by the Pre-Columbian Maya civilization.

The numerals are made up of three symbols; zero (shell shape), one (a dot) and five (a bar). For example, nineteen (19) is written as four dots in a horizontal row above three horizontal lines stacked upon each other.

1500

Da Vinci was a genius: painter, musician, sculptor, architect, engineer, and … the list goes on. However, his contributions to mechanical calculation remained hidden until the rediscovery of two of his notebooks in 1967. These notebooks, which date from sometime around the 1500s, contained drawings of a mechanical calculator, and working models of da Vinci's device have since been constructed.

 

Actually, it should be noted that some people believe that these sketches represent nothing more than a gear train, and that building a calculator based on them requires a certain amount of wishful thinking and extrapolation.

1614

John Napier describes the nature of logarithms. he also builds Napiers bone, the forerunner to the slide rule.

Napier, who is credited with the invention of logarithms, only considered the study of mathematics as a hobby. Napier’s discussion of logarithms appears in his Minifici Logarithmorum Canonis Descriptio (1614). Unlike the logarithms used today, Napier’s original logarithms are to base 1/e and involve a constant (10^7). Napier defined his logarithms as a ratio of two distances in a geometric form, as opposed to the current definition of logarithms as exponents. What was Napier’s purpose for inventing this system? He developed this shortcut to save astronomers time and limit "slippery errors" of calculations. His idea was that by "shortening the labors, doubled the life of the astronomer." With his logarithms, Napier presented a mechanical means of simplifying calculations in his Rabdologiae in 1617. He described a method of multiplication using rods with numbers marked off on them. This was the earliest form of mechanical calculation and the forerunner of our modern day calculator.

1621

William Oughtred invent the slide rule, which does not become obsolete for nearly 350 years.

William Oughtred (5 March 1574 – 30 June 1660) was an English mathematician.

After John Napier invented logarithms, and Edmund Gunter created the logarithmic scales (lines, or rules) upon which slide rules are based, it was Oughtred who first used two such scales sliding by one another to perform direct multiplication anddivision; and he is credited as the inventor of the slide rule in 1622. Oughtred also introduced the "×" symbol for multiplication as well as the abbreviations "sin" and "cos" for the sine and cosine functions.

1642

Blaise Pascal invents Pascaline, the first mechanical calculator. It was hand turned and could only add and substract.

Blaise Pascal, the French scientist was one of the most reputed mathematician and physicist of his time. He is credited with inventing an early calculator, amazingly advanced for its time. A genuis from a young age, Blaise Pascal composed a treatise on the communication of sounds at the age of twelve, and at the age of sixteen he composed a treatise on conic sections.

1670

Eleven years after the death of Blaise Pascal, a young and energetic German lawyer by the name of Gottfried Wilhelm von Leibniz, who lived from 1646-1716, began to develop an improved version of the Pascaline automatic calculator.

Gottfried Wilhelm von Leibniz

Unlike Pascal, von Leibniz was able to successfully introduce an automatic calculator into the business marketplace of his day. Originally designed in 1673 and first built in 1694, the Leibniz Calculator had the ability to add, subtract, multiply, and divide. By using wheels placed at right angles which could be displaced by a special stepping mechanism, it could perform rapid multiplication or division. Just as with the Pascaline, the Leibniz Calculator required that the operator using the device had to understand how to turn the wheels and thus, know the "programming language" of the calculator.

 Leibniz Calculator

1679

Leibniz Introduces binary arithmetic

The binary numeral system, or base-2 number system represents numeric values using two symbols,0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2. Owing to its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used internally by all modern computers.

This is the end of part 1 of Computer History series. I’ll be write the next part. Be patient